Introduction

In the world of statistics, hypothesis tests are powerful tools used to evaluate the validity of assumptions or ideas based on data. Imagine you're the coach of a professional football team, faced with a decision regarding the performance of two players. One player, the new sensation, has a remarkable scoring rate with five goals in two matches. On the other hand, the current star player has a scoring rate of one goal per match but has played 100 matches. You find yourself in a dilemma – is the new player truly a better scorer, or is this just a lucky streak? Hypothesis tests can help you make informed decisions.

Common Tests

Hypothesis tests come in various forms, each suited for different types of data and situations. Here, we'll explore some commonly used ones:

1. One Sample T-Test

   The one-sample t-test is designed to assess differences between a sample and the entire population from which that sample is drawn. In our football scenario, it can answer questions like, "Is the average number of goals scored by my team higher than that of the entire league?"

2. Independent Samples T-Test

   An independent samples t-test compares two different samples to determine if there are significant differences between them. As the football coach, you might wonder, "Is the average number of goals scored by my team higher than that of our rival team?"

3. Paired Samples T-Test

   A paired samples t-test assesses differences within the same sample at different points in time. This test is handy for questions such as, "Has the average number of goals scored by my team increased after our 4-week training program?"

4. Chi-Square Test of Independence

   The chi-square test of independence is used when you want to establish if there's a significant relationship between two categorical variables. For example, as the football coach, you might ask, "Is the penalty kick success rate of my newly signed player higher than that of my current star player?"

The Setup

Before conducting a hypothesis test, it's essential to establish three key elements:

• Null Hypothesis

  The null hypothesis represents your initial assumption, often assuming that the result is purely due to chance or that there is no relationship between two variables. In our context, it would be something like, "There's no significant difference in the goal-scoring rates of the new and current players."

• Alternate Hypothesis

  The alternate hypothesis contradicts the null hypothesis, suggesting that the result is not by chance or that there is indeed a relationship between two variables. For instance, it could be, "The new player's goal-scoring rate is significantly higher than that of the current star player."

• Acceptance Criteria

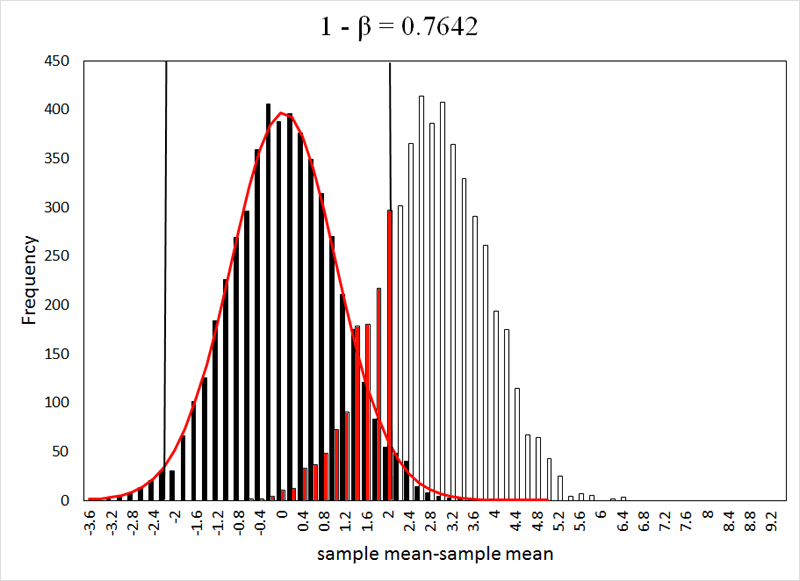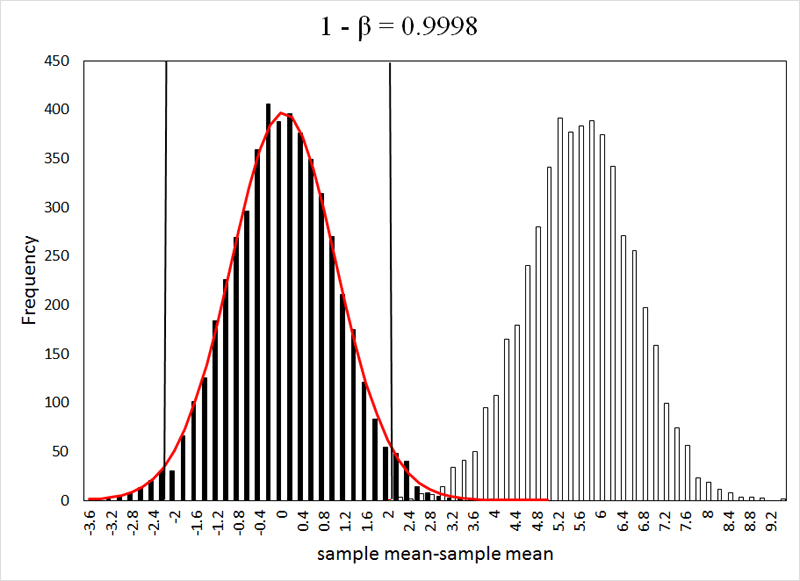
  The acceptance criteria determine when there is enough evidence to support the null hypothesis. Commonly set at a p-value of 0.05 (5%), it can be adjusted for higher certainty. A lower p-value indicates stronger evidence against the null hypothesis.

Let's Talk about P-Values

The outcome of a hypothesis test heavily relies on the acceptance criteria, often expressed as a p-value. Understanding p-values is crucial:

What a P-Value Is: A p-value helps assess whether the results are likely to be ordinary or extraordinary. A p-value of 0.05 means there's a 5% or lower chance that the result occurred by chance.

What a P-Value Is Not: It's not a probability of an event happening but a measure of the likelihood of obtaining different results if the test were repeated many times. It also doesn't tell you how different two samples are; instead, it indicates how confident you can be that they are different.

In conclusion, hypothesis tests are invaluable tools for making data-driven decisions in various fields, including sports like football. They allow us to assess the validity of assumptions, make comparisons, and draw conclusions based on evidence, all while considering the probability of results occurring by chance. So, whether you're a football coach evaluating player performance or a scientist conducting experiments, hypothesis tests help you navigate the uncertain waters of data analysis.